Introduction
La vie quotidienne nous offre de nombreuses occasions qui nous permettent de développer le raisonnement mathématique chez notre enfant. Les jeux, les discussions et les observations permettent aux enfants d’apprendre en s’amusant. Lorsqu’on en prend conscience, les petits gestes du quotidien se transforment donc en occasions riches et variées pour apprendre. Dans cet article, découvrez comment soutenir de façon concrète les apprentissages de votre enfant en mathématiques.
Souvent, on associe les mathématiques à des notions précises, à un vocabulaire parfois difficile à comprendre et à des procédures qu’on applique à la lettre. On peut même avoir l’impression que les mathématiques ne sont pas accessibles à tous, alors que c’est faux. En fait, les mathématiques sont bien plus qu’une science : elles sont présentes au cœur de notre quotidien. Alors, que vous soyez à la maison, en voiture ou au supermarché, découvrez de nombreuses occasions pour aider votre enfant à développer son raisonnement mathématique au-delà des activités proposées dans les devoirs. N’ayez pas peur de sortir certains accessoires de bricolage pour illustrer des notions. Il est possible de rendre concret ce qui l’est moins pour un enfant.
Voici quelques exemples de petits gestes du quotidien qui permettent de soutenir le raisonnement mathématique.
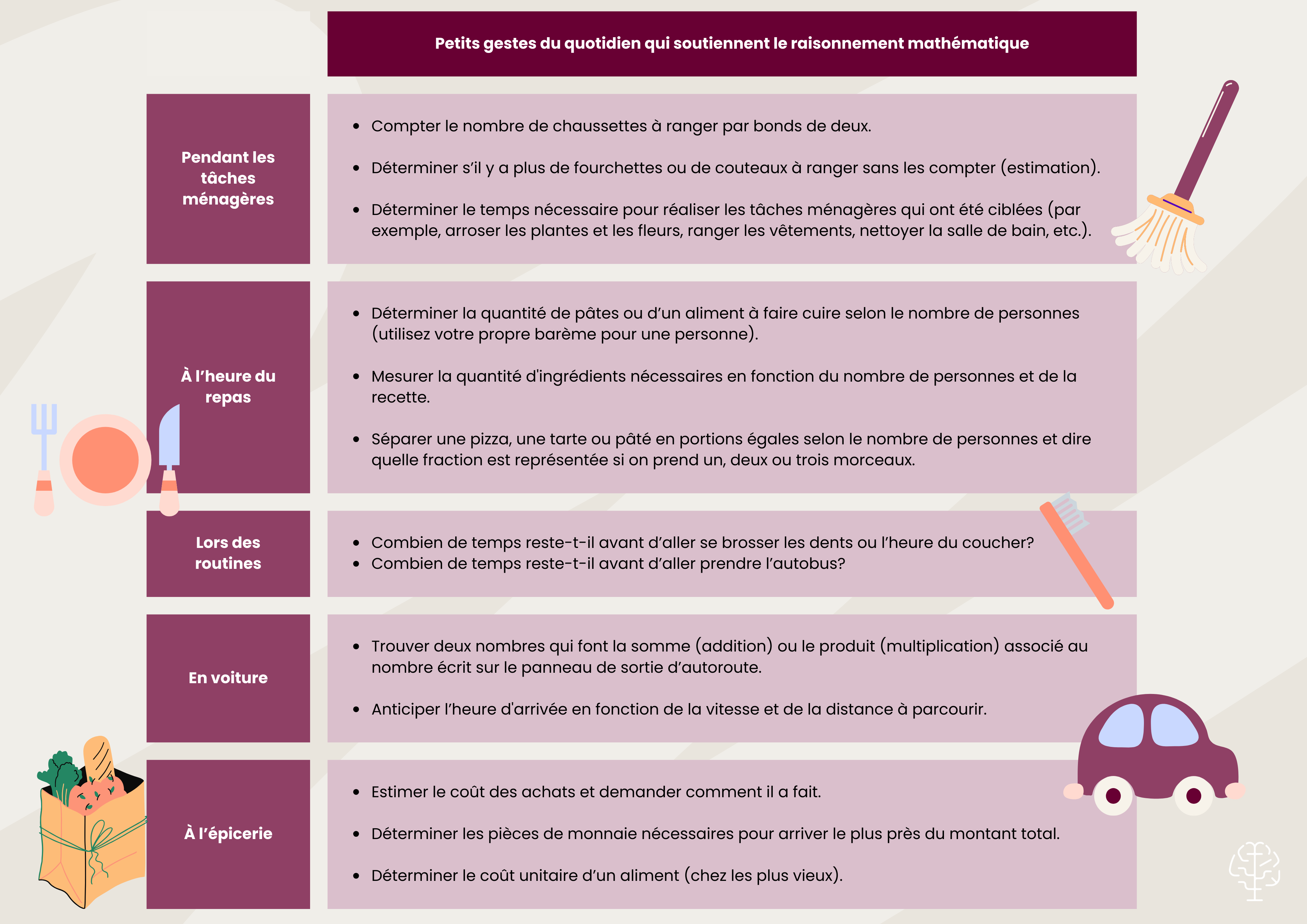
Rendre les apprentissages concrets
Pour faire des groupements, on peut utiliser des goupilles qu’on regroupe en paquet de 10 dans un sac hermétique. Pour représenter le nombre 27, votre enfant devrait regrouper 10 goupilles dans un premier sac et 10 autres dans un deuxième. Ensuite, les 7 goupilles restantes seront laissées de côté pour illustrer les unités. On développe donc le dénombrement et le groupement. On peut également effectuer des opérations sur les nombres naturels avec des bâtonnets (centaines), des cure-pipes (dizaines) et de petits pompons (unités). Par exemple, on pourrait demander à son enfant d’effectuer l’opération 93 + 28 = ▢. À ce moment, il devra représenter ces deux nombres, puis faire les regroupements nécessaires pour trouver la somme à partir des objets. N’ayez pas peur d’utiliser différents objets ou de changer la valeur de ceux-ci.
On peut également utiliser des jetons ou de petits cubes pour représenter certaines régularités comme les nombres premiers ou les nombres carrés. Pour comprendre le concept de nombre carré, on peut demander à son enfant de placer les petits cubes de sorte qu’il y en ait un nombre égal de chaque côté. Par exemple, pour le chiffre 9, on fera 3 rangées de 3, ce qui représente un carré.
Souvent, il est difficile pour les jeunes apprenants de trouver le terme manquant dans une opération mathématique. On peut donc utiliser des jetons pour résoudre une équation avec un inconnu. Par exemple, avec l’équation 8 + ▢ = 17, on pourrait demander à son enfant ce qu’il va faire avec ses jetons pour trouver le terme manquant. Ici, on développe différentes stratégies de calcul mental en plus de développer la pensée préalgébrique.
Pour représenter la partie d’un tout ou pour effectuer des opérations sur les fractions, l’utilisation de matériel peut aider votre enfant à comprendre la notion de parties égales dans les fractions. On peut utiliser des bandes de papier, des jetons, des disques ou des réglettes. Par exemple, la fraction 4/7 peut être représentée par une bande de papier séparée en 7 parties égales dont 4 sont coloriées. On pourrait comparer des bandelettes de même longueur, mais séparées différemment. Cela peut aider votre enfant à mieux comprendre les fractions équivalentes. L’utilisation de matériel est également utile pour illustrer les opérations sur les fractions. Il peut donc servir d’appui pour compléter des activités de type papier-crayon.
On peut répéter les mêmes activités avec le même matériel utilisé pour représenter les nombres naturels. Votre enfant devra donc faire les groupements appropriés pour former des dixièmes à partir de centièmes ou des unités à partir de dixièmes par exemple. On peut également utiliser un tableau de numération à l’appui pour aider son enfant à placer les chiffres à la bonne position lorsque vient le temps d’effectuer des opérations sur les nombres décimaux.
Est-ce que 52 se divise par 4? Par 6? Ici, l’utilisation de matériel comme des jetons ou de petits cubes peut aider votre enfant à répondre rapidement à cette question. Il devra former des groupes égaux pour déterminer si un nombre se divise par tel ou tel nombre. Cela l’aidera à découvrir la règle par lui-même au lieu de se fier uniquement à sa mémoire : l’apprentissage sera donc plus durable et plus significatif.
Dans tous les cas, le matériel de manipulation peut soutenir le passage du mode concret (avec matériel), vers le mode imagé (dessin, image, tableau), vers le mode symbolique (nombres, équations et algorithmes). On peut donc passer d’un mode à l’autre pour consolider certaines notions qui sont plus difficiles à apprendre.
Pour aller plus loin
Bay-Williams, J. et KING, J.; adaptation St-Pierre, A. (2023). Développer la fluidité en mathématiques: stratégies, jeux et outils d’évaluation pour favoriser la maitrise des faits numériques, Montréal. Chenelière éducation, p. 176 (didactique, sciences et mathématiques).
Charbonneau, C. (2019). La manipulation en mathématique au cœur des apprentissages : activités et conseils pour un enseignement plus concret, Montréal. Chenelière éducation, p. 198 (didactique, sciences et mathématiques).
Van de Walle, J. A. et Lovin, L. H. (2007). L’enseignement des mathématiques: L’élève au centre de son apprentissage: du préscolaire à la première année du deuxième cycle du primaire, Montréal. ERPI, tome 1, p. 416(collection).
Un peu plus sur l'autrice
Marie-Lou a commencé sa carrière dans le monde de l’éducation en tant qu’enseignante en adaptation scolaire. Rapidement, elle s’est intéressée à l’orthopédagogie, domaine dans lequel elle s’est spécialisée au cours des 15 dernières années. De plus, elle a agi en tant que conseillère pédagogique pour outiller les enseignants dans l’adoption de pratiques d’enseignement inclusives et différenciées en salle de classe ordinaire. Marie-Lou a également contribué à la mise en place d’outils d’aide à la lecture et à l’écriture pour soutenir les élèves rencontrant des défis d’apprentissage.










.png)


